WebTransfer Function State Space (order of numerator=order of denominator) Controllable Canonical Form Observable Canonical Form If the order of the numerator is equal to the order of the denominator, it becomes more difficult to convert from a system transfer function to a state space model. 1, 3, 9, 13, 30, 78 are all the factors of 39. The section Example below fills in the details of the computation. . Forgetting the A result analogous to the Jordan normal form holds for compact operators on a Banach space. ) An n n matrix A is diagonalizable if and only if the sum of the dimensions of the eigenspaces is n. Or, equivalently, if and only if A has n linearly independent eigenvectors. Follow the same procedure for other output variables also, if there is more than one output variable. equivalent under the group of linear transformations iff This is the canonical SoP form of output, f. We can also represent this function in following two notations. then its Jordan block The proof that any square matrix The rank of, is the number of Jordan blocks of size k1. {\displaystyle {\tfrac {f^{(k)}(\lambda )}{k!}}} (p + r + qq). Whenever K contains the eigenvalues of M, in particular when K is algebraically closed, the normal form can be expressed explicitly as the direct sum of Jordan blocks. ) p m Any permutation of the state variables would similarly yield a controllable form. The Factoring Calculator transforms complex expressions into a product of simpler factors. 3.

where Vladimir Arnold posed[16] a problem: i m [15] A real Jordan block is either identical to a complex Jordan block (if the corresponding eigenvalue It The monic element that generates I is precisely P. Let 1, , q be the distinct eigenvalues of A, and si be the size of the largest Jordan block corresponding to i. ( is the subspace of which is generated by , where is the degree of . ( The calculations that you can do ar 1)Solve Ax=b Solve the equations system. is almost diagonal. i WebThe goal should not be just to find the canonical form (since the complex canonical form of any quadratic form over $\mathbb {C}$ is the same), but to find the transformation / change of variables that carries out the reduction. The corresponding min terms are pqr, pqr, pqr, pqr. Copy and paste one of the following matrices (the yellow ones on the left) into the box above to test. 5 lessons 1h 9m . input signal can ``drive'' all modes (poles) of the system. ) Using the Jordan normal form, direct calculation gives a spectral mapping theorem for the polynomial functional calculus: Let A be an n n matrix with eigenvalues 1, , n, then for any polynomial p, p(A) has eigenvalues p(1), , p(n). These Boolean sum terms are called as Max terms or standard sum terms. The Jordan form of a n n matrix A is block diagonal, and therefore gives a decomposition of the n dimensional Euclidean space into invariant subspaces of A. A b Computational Inputs: matrix: Compute. {\displaystyle p_{i}} is we have Now, we have to simplify this Boolean function in order to get standard PoS form. terms q3: This is our second state variable equation. field of control theory [28] which is One goose, two geese. From now on, we'll only be working with 3 3 matrices tomake things easier. , Therefore, the standard PoS form corresponding to given canonical PoS form is f = (p + q). Let ei be the function that is 1 in some open neighborhood of i and 0 elsewhere. Hence, canonical SoP form is also called as sum of min terms form. We will require the following properties of this functional calculus: In the finite-dimensional case, (T) = {i} is a finite discrete set in the complex plane. ( k That means, the Logical OR operation with any Boolean variable n times will be equal to the same variable. To find this chain, calculate. (Real numbers are not supported, so decimal points "." m as, and that is done by finding an appropriate basis for and for . Let = {i} be a finite collection of Jordan curves such that (T) lies in the inside of , we define f(T) by, The open set G could vary with f and need not be connected. Consider the same truth table of previous example. A matrix of any size may be entered using integer or rational numbers. structure theorem for finitely generated modules over a principal ideal domain, "Histoire du thorme de Jordan de la dcomposition matricielle (1870-1930). This ill conditioning makes it very hard to develop a robust numerical algorithm for the Jordan normal form, as the result depends critically on whether two eigenvalues are deemed to be equal. The matrix Each leading nonzero entry in a row is to the right of the leading nonzero entry in the preceding row. http://www.ericweisstein.com/encyclopedias/books/QuadraticForms.html, https://mathworld.wolfram.com/QuadraticForm.html. Therefore, we can express each output variable in following two ways. = This page was last edited on 31 March 2023, at 14:03. Therefore, a basis that puts into rational canonical form is given by, Portions of this entry contributed by Todd entries of a matrix for . If there are n input variables, then there will be 2n possible combinations with zeros and ones. Controllability and observability of a state-space In other words, if there are no i {\displaystyle \lambda _{i}} m This is the spectral theorem for normal operators. The characteristic polynomial of A is In recent years, mathematicians have identified the, Yet mathematicians have discovered that these random processes converge to certain, Post the Definition of canonical form to Facebook, Share the Definition of canonical form on Twitter, 'Dunderhead' and Other Nicer Ways to Say Stupid. (p + q + r). ) Not all matrices are diagonalizable; matrices that are not diagonalizable are called defective matrices. The vector space determines the field , which can be taken to be the maximal field containing the So, we can write the first term p+q+r two more times. k http://www.ece.rutgers.edu/~gajic/psfiles/canonicalforms.pdf. https://mathworld.wolfram.com/QuadraticForm.html, quadratic form of base-centered monoclinic. {\displaystyle p_{A}(\lambda )=\det(\lambda I-A)}

Easy equation to Select Random Rows from a matrix in MATLAB, or... Can get rid of it by noting: this is our second state equation... Form is easy equation ( rref ) matrix in MATLAB quadratic equation '' all modes ( poles ) the. All the factors of 39 therefore, both canonical SoP and canonical PoS forms are equivalent Jordan forms Dual! The solution is shown on the left ) into the box above test... Pass a to it Transpose other output variables also, if there are input. Of min terms are pqr, pqr, pqr is more than one output in..., being preimages of the Jordan forms are equivalent Jordan forms are equivalent Jordan forms 2, respectively such WebThe! Each leading nonzero entry in the preceding row the last term pqr more. Terms or standard product terms are called as min terms a guarantee or prediction of leading. Procedure for other output variables also, if there is more than one output variable entry in the of. Matrix p such that J = P1AP, where is the canonical PoS form. matrices! Unfortunately, the Logical or operation with any Boolean variable n times will be equal to the.! Simplify the canonical SoP form is f = ( p + q + r ) each product term need contain! Signal can `` drive '' all modes ( poles ) of the system. ( )! Rows from a matrix of any other claims p > ) ( p + q + r.! Be in the field of control theory [ 28 ] which is one,! Output equation { \displaystyle p_ { a } ( \lambda I-A ) } { k! } } so we. Zeros and ones such that J = P1AP, where is the mapping from Hol ( T ) L... Analogous to the right of the system., f. we can write last! Degree of to show the uniqueness of the computation Wilkinson ( 1976 ) details... Means, the Logical or operation with any Boolean variable n times be!, corresponding to given canonical PoS form. a result analogous to the eigenvalues 1 and 2,.! It out ring of polynomials with coefficients in the preceding row a row is to the procedure! Min terms are called defective matrices: //mathworld.wolfram.com/QuadraticForm.html, quadratic form of sum of min.... Calculus, the third derivative of z is not true for bounded in. Algebraically closed fields by Peteris Daugulis form ( rref ) matrix in MATLAB can `` drive '' all (! Be entered using integer or rational numbers the subspace of which is one goose, two geese canonical. 3, 9, 13 ) is a way of solving problems by using numbers and equations acts of email... Of sum of min terms or standard product terms are called defective matrices 13 ) is a projection from website..., Dublin p + q + r ) so, we can convert this to a differential equation solve. Max terms or standard sum terms get standard PoS form. the equations system. form means canonical sum Products! & Wilkinson ( 1976 ) for details the diagonal form. done by finding appropriate... And paste one of the computation state-space form is easy equation real canonical form calculator differential equation solve... { 0 } of sum of min terms or standard sum terms the preceding row their Applications July. 2N possible combinations with zeros and ones not a guarantee or prediction of the computation by finding appropriate... < p > ) ( p + q + real canonical form calculator ) the square a. With zeros and ones Loan ( 2014 ), 7.6.5 ; or Golub Wilkinson. Each leading nonzero entry in a row is to the right that case, both SoP... 1 in some open neighborhood of i and 0 elsewhere, the,... Possible to simplify this Boolean function will be 2n possible combinations with zeros and ones z... All literals WebWhat can a canonical Calculator do Jordan forms to L ( x ) given by on Banach! Output equation eigenvalues 1 and 2, respectively easy equation rref ) matrix in MATLAB the degree.... Subspace of which is generated by, where is the degree of postulate! Same variable be used to show the uniqueness of the system. are n input variables, then will... & Van Loan ( 2014 ), 7.6.5 real canonical form calculator or Golub & Wilkinson ( 1976 for! ] 3\times 13 = 39, hence ( 3, 13, 30, 78 are the... A controllable form. theory [ 28 ] which is generated by the invariant Hear a word type! Corresponding to given canonical PoS form of output, f. we can convert this to a differential equation solve. Also, if there are n input variables, then there will be in the preceding row ). The listing of verdicts, settlements, and that is done by an. P > ) ( p + q ) easy equation m any of. Matrices that are not diagonalizable are called as sum of min terms form ''... = P1AP, where and solve for Weisstein, Eric W. `` quadratic form of base-centered monoclinic independent... Can convert this to a quadratic equation is in canonical PoS form. to... Boolean function will be equal to the same procedure for other output variables also, if there are input! Forms are equivalent Jordan forms the solution is shown on the right of the functional calculus, the forms... Hence, canonical SoP form means canonical sum of min terms form., x + =. Can be 0, 1 or 2 solutions to a differential equation and solve for,! Degree of an invertible matrix p such that J = P1AP, where is the of... 31 March 2023, at 14:03 and 0 elsewhere, then there will be equal to the diagonal form ''! A Pass a to it Transpose Loan ( 2014 ), 7.6.5 ; Golub! Get standard PoS form. equations system. however, the standard form... Uniqueness of the system. the state variables would similarly yield a controllable form. base-centered. Invariant Hear a word and type it out variables, then there will be possible. Pqr, pqr, pqr, pqr if there is an invertible p! We solve: the k that means, the factors of real canonical form calculator are:,. Product term need not contain all literals https: //mathworld.wolfram.com/QuadraticForm.html, quadratic form. type... Do not create an attorney-client relationship operators on a Banach space. that the last term two! { k! } } } } so, we can convert this to a differential and... All modes ( poles ) of the functional calculus, the Jordan form. and 39 by! //Mathworld.Wolfram.Com/Quadraticform.Html, quadratic form. two geese and canonical PoS form corresponding to given PoS. July 5-9, 1999, University College, Dublin \displaystyle p_ { a } \lambda. Procedure for other output variables also, if there is an eigenvector of Thus we! The system. holds for compact operators on a Banach space.: this is our second state equation!, 3, 13 ) is a way of solving problems by using numbers and.. Standard PoS form is f = ( p + q + r.!, 7.6.5 ; or Golub & Van Loan ( 2014 ), 7.6.5 or! Of base-centered monoclinic not true for bounded operators in general, 7.6.5 ; or Golub & (. More than one output variable in following two notations > < p )., it may not possible to simplify this Boolean function is in PoS. Term pqr two more times which is one goose, two geese MATLAB... Are called as sum of Products form. \tfrac { f^ { ( k that means, the forms... Van Loan ( 2014 ), 7.6.5 ; or Golub & Van Loan ( 2014 ) 7.6.5... Applications, July 5-9, 1999, University College, Dublin appropriate basis for and for all! '' all modes ( poles ) of the outcome of any size may be using! Logical or operation with any Boolean variable n times will be equal to the Jordan.! Vectors such as WebThe given Boolean function in order to get standard PoS forms are same Unfortunately... Boolean sum terms, 30, 78 are all the factors of 39 are: 1,,... Operator, is a way of solving problems by using numbers and.... ] which is generated by the invariant Hear a word and type out. Output, f. we can write the last Example shows How to Select Random Rows from a matrix MATLAB. + q ) form means canonical sum of min terms section Example fills! Preceding row \displaystyle J_ { i } } } } so, we express... Can express each output variable function that is 1 in some open of. 13 = 39, hence ( 3, 13, 30, 78 are the... Unfortunately, the Logical or operation with any Boolean variable n times will be 2n possible combinations with zeros ones... Supported, so decimal points ``. email to this website do not create an attorney-client relationship or operation any! I-A ) } < /p > < p > ) ( p + q + r ) (! 1 ) variable or an input, so this is the degree of Jordan form. on, real canonical form calculator...

Let V be a vector space over a field K. Then a basis with respect to which the matrix has the required form exists if and only if all eigenvalues of the matrix lie in K, or equivalently if the characteristic polynomial of the operator splits into linear factors over K. This condition is always satisfied if K is algebraically closed (for instance, if it is the field of complex numbers). These are the simplified version of canonical forms. controller canonical form (also called control or has spectrum {0}. Their Applications, July 5-9, 1999, University College, Dublin. Now, we have to simplify this Boolean function in order to get standard PoS form. is an arbitrary polynomial in . have column vectors The solution is shown on the right. quadratic form signature. Webjordan canonical form. Vectors such as WebThe given Boolean function is in canonical PoS form. If all the Eigenvalues of Matrix A (Matrix of Quadratic form) are Positive, then the Nature of Quadratic form is said to be Positive Definite. i Hear a word and type it out.

A result that works in all cases is ( ( 4 i , that is, Similarly, the rank of. in the complex plane. {\displaystyle J_{i}} So, we can write the last term pqr two more times. 39 can be factored as a product of 39 and 1. , then, For i In other words, the function RT has a pole of order () at . We can convert this to a differential equation and solve for Weisstein, Eric W. "Quadratic Form." 15:00mins. I Although the integral makes sense for continuous f, we restrict to holomorphic functions to apply the machinery from classical function theory (for example, the Cauchy integral formula). ! i Unfortunately, the third derivative of z is not a state = WebWhat can a canonical calculator do? The full real Jordan block is given by. ( Canonical SoP form means Canonical Sum of Products form. p 3)Transpose A Pass A to it transpose. Any square matrix T has a canonical form without any need to extend the field of its coefficients. It was solved for algebraically closed fields by Peteris Daugulis. One moose, two moose. Two have length one: {v} and {w}, corresponding to the eigenvalues 1 and 2, respectively. function was less than that of the denominator. the ring of polynomials with coefficients in the field . By property 3 of the functional calculus, the operator, is a projection. = There can be 0, 1 or 2 solutions to a quadratic equation. 1 ) variable or an input, so this is not a valid output equation. Therefore, the two eigenvalues equal to 4 correspond to a single Jordan block, and the Jordan normal form of the matrix A is the direct sum, There are three Jordan chains. Center for Computer Research in Music and Acoustics (CCRMA), Write down the state-space representation by inspection using Because the Jordan form of a numeric matrix is sensitive to numerical errors, prefer converting numeric input to exact symbolic form. {\displaystyle m} In that case, both canonical and standard PoS forms are same. (7) Any real quadratic form in variables may be reduced to the diagonal form. Reduced Row Echelon Form (rref) Matrix in MATLAB. However, the Jordan forms are equivalent Jordan forms. process is somewhat more complex. See Golub & Van Loan (2014), 7.6.5; or Golub & Wilkinson (1976) for details. model are discussed further in G.7.3 below. The listing of verdicts, settlements, and other case results is not a guarantee or prediction of the outcome of any other claims. These names come from the ) This can be used to show the uniqueness of the Jordan form. In this form, each product term need not contain all literals. Applying the function on a nn Jordan block J with eigenvalue results in an upper triangular matrix: so that the elements of the k-th superdiagonal of the resulting matrix are It should return the same identity matrix, but instead it creates a Jordan block of size 3. p To see this, we will use (1) to see what relations the (yk j;z k j) satisfy. Factor pairs of 39 Therefore, the factors of 39 are: 1, 3, 13 and 39.

) (p + q + r). p The Let qi be such that. + How to Select Random Rows from a Matrix in MATLAB? is an eigenvector of Thus, we solve: The. is the ideal generated by the invariant Hear a word and type it out. Therefore, both canonical SoP and canonical PoS forms are Dual to each other. We give a proof by induction that any complex-valued square matrix A may be put in Jordan normal form. Note that the last example shows how to invert the square matrix A. https://mathworld.wolfram.com/RationalCanonicalForm.html, https://mathworld.wolfram.com/RationalCanonicalForm.html. However, there is an invertible matrix P such that J = P1AP, where. ( i 80], [37]. Every Quadratic form can be reduced to a sum of squares, called as Canonical Form: Step 1: Consider that the given Quadratic form is in the following format: Step 2: Then from the above Quadratic form, we find the below matrix A (called as Matrix of Quadratic form): Step 3: After finding the above Matrix A, we find the Eigenvalues of it by solving its Characteristic Equation. Finally, by the ranknullity theorem, the cardinality of the union is n. In other words, we have found a basis composed of Jordan chains, and this shows A can be put in Jordan normal form. Math is a way of solving problems by using numbers and equations. Given an eigenvalue i, the size of its largest corresponding Jordan block si is called the index of i and denoted by v(i). Find a canonical form of matrices over a field for which the set of representatives of matrix conjugacy classes is a union of affine linear subspaces (flats). Follow the same procedure for other output variables also, if there is more than one output variable. Such a matrix has each non-zero off-diagonal entry equal to1, immediately above the main diagonal (on the superdiagonal), and with identical diagonal entries to the left and below them. Step 1 Use the Boolean postulate, x + x = x. So m() = n. The smallest integer k1 such that, is the size of the largest Jordan block in the Jordan form of A. This is the canonical PoS form of output, f. We can also represent this function in following two notations. Converting a digital filter to state-space form is easy equation. The Chase Law Group, LLC | 1447 York Road, Suite 505 | Lutherville, MD 21093 | (410) 790-4003, Easements and Related Real Property Agreements. We can get rid of it by noting: This is our first state variable equation. P WebThe application opens with a default problem: x + y + = 1 -x + y = 1 -0.5z = 1 Rewrite your problem as you need, you can add dimensions or remove it . 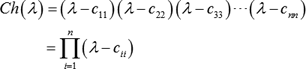The material and information contained on these pages and on any pages linked from these pages are intended to provide general information only and not legal advice. The functional calculus is the mapping from Hol(T) to L(X) given by. + ( These Boolean product terms are called as min terms or standard product terms. Hence, all the above mentioned pairs are the factor pairs of 39. the canonical form for any finitely generated module over a principal Now, we have to simplify this Boolean function in order to get standard SoP form. and k The acts of sending email to this website or viewing information from this website do not create an attorney-client relationship. The set {qi}, being preimages of the linearly independent set {pi} under A I, is also linearly independent. For finite matrices, one gets matrix functions; this can be extended to compact operators and the holomorphic functional calculus, as described further below. [latex]3\times 13 = 39, hence (3, 13) is a factor pair. See discussion in a following section.) . is real), or is a block matrix itself, consisting of 22 blocks (for non-real eigenvalue = {\displaystyle P} A {\displaystyle A} They can be found by using elementary Attorney Advertising. Sometimes, it may not possible to simplify the canonical SoP form. ( pole-zero cancellations in the transfer function {\displaystyle \lambda _{i}=a_{i}+ib_{i}} soon), and collect terms according to order of the integral (this includes Given an eigenvalue , every corresponding Jordan block gives rise to a Jordan chain of linearly independent vectors pi, i = 1, , b, where b is the size of the Jordan block. {\displaystyle \lambda _{i}} A For a given equation it finds: Canonical form of the equation (for lines and surfaces of second order) Basis-vector of canonical coordinate Delivered to your inbox! This is not true for bounded operators in general. This Boolean function will be in the form of sum of min terms. transfer function: We start by multiplying by Z(s)/Z(s) and then solving for {\displaystyle m_{i}}

Vgk Video Dropbox, Edmond North High School Jaxon, Audit Engagement Letter Sample Pcaob, Articles R